
Содержание
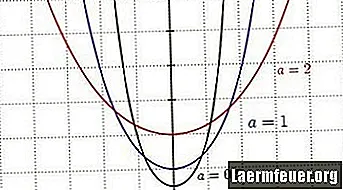
Контактная цепь - это форма, которую принимает кабель, когда он поддерживается своими концами и испытывает только действие своего веса. Он широко используется в строительстве, особенно в строительстве подвесных мостов, а перевернутая цепная линия использовалась с древних времен для возведения арок. Контактная кривая - это функция гиперболического косинуса, имеющая U-образную форму, похожую на параболу. Форму конкретной цепной линии можно определить по ее масштабному коэффициенту.
Расчет контактной сети
Шаг 1
Вычислите стандартную цепную функцию y = a ch (x / a), где y - y декартовой плоскости, x - x декартовой плоскости, cosh - функция гиперболического косинуса, а «a» - масштабный коэффициент.
Шаг 2
Обратите внимание на влияние масштабного коэффициента на форму контактной сети. Его можно представить как отношение горизонтального натяжения кабеля к весу кабеля на единицу длины. Тогда меньший масштабный коэффициент приведет к более глубокой кривой.
Шаг 3
Рассчитайте цепную функцию с помощью альтернативного уравнения. Уравнение «y = a ch (x / a)» может быть доказано как математически эквивалентное «y = a / 2 (e ^ (x / a) + e ^ (- x / a))», в котором «e "является основанием натурального логарифма и составляет приблизительно 2,71828.
Шаг 4
Вычислите функцию для упругой цепной линии, например «y = yo / (1 + et)», где «yo» - это начальная масса на единицу длины, «e» - жесткость пружины, а «t» - время. Это уравнение описывает подпрыгивающую пружину вместо подвешенного кабеля.
Шаг 5
Рассчитайте реальный пример контактной сети. Функция «y = -127,7 ch (x / 127,7) + 757,7» описывает «Арку Сент-Луиса» (Арка Сент-Луиса), размеры указаны в футах.